Методы расчета сложных электрических цепей постоянного тока

1. Метод узловых и контурных уравнений

В основе расчета лежат первый и второй законы Кирхгофа.

                                              ∑I=0

                                              ∑E=∑IR

Порядок расчета

1. Произвольно выбираем направление тока в ветвях.
2. Произвольно выбираем направление обхода контуров.
3. Зная полярность источников, проставляем направление ЭДС.
4. Составляем уравнения по первому закону Кирхгофа. Их должно быть но одно меньше, чем узлов.
5. Составляем уравнения по второму закону Кирхгофа из расчета, что общее число уравнений должно быть равно числу неизвестных токов.
6. Решаем систему уравнений и определяем неизвестные токи. Если в результате решения какой-либо ток окажется со знаком «-», то направление его противоположно выбранному.

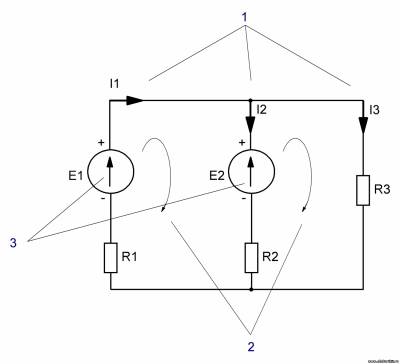
Приведем пример.

Дано:

18. ₁=r₂=0;
18. ₁=0,3 Ом;
18. ₂=1 Ом;
18. ₃=24 Ом;

Е₁=246 В;

Е₂=230В

Найти:

I₁,I₂,I₃.

Решение:

Итак, на схеме рисуем направления токов (1), согласно этим направлениям рисуем направления обхода контуров (2), согласно полярности источников питания ставим направления ЭДС (3).

Согласно первому закону Кирхгофа:

                                    I₁-I₂-I₃=0 → -I₂=I₃-I₁

Теперь составляем уравнения по второму закону Кирхгофа:

                                               E₁=I₁R₁+I₃R₃

                                               Е₂=-I₂R₂+I₃R₃

Получили систему из трех уравнений. Решаем.

                                              E₂=(I₃-I₁)R₂+I₃R₃

                                             230=I₃(1+R₃)-I₁=25I₃-I₁ → I₁= 25I₃-230

                                             E₁=I₁R₁+I₃R₃=(25I₃-230)R₁+I₃R₃

                                           246=0,3(25I₃-230)+24I₃

                                           246=7,5I₃-69+24I₃

                                           31,5I₃=315

                                           I₃=10A

                                           I₁=25∙10-230=20A

                                           I₂=I₁-I₃=20-10=10A

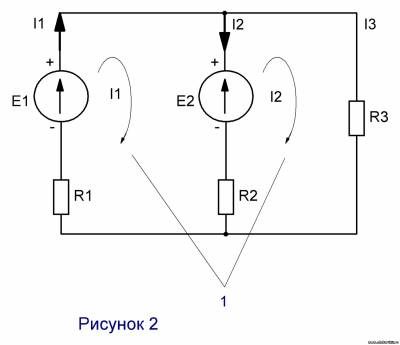
2. Метод контурных токов

Этот метод основан на втором законе Кирхгофа

1. Произвольно выбираем направления контурных токов (рис.2)
2. Составляем уравнения по второму закону Кирхгофа.

                                         E₁-E₂=I₁(R₁+R₂)-I₂R₂

                                         E₂=I₂(R₂+R₃)-I₁R₂

                                         246-230=I₁(0,3+1)-I₂ → 16=1,3I₁-I₂ → I₂=1,3I₁-16

                                         230=25(1,3I₁-16)-I₁

                                         31,5I₁=630

                                          I₁=20A

                                          I₂=1,3∙20-16=10A

3. Определяем истинные токи.

                                         I₁=I₁=20A

                                          I₂=I₁-I₂=10A

                                          I₃=I₂=10A

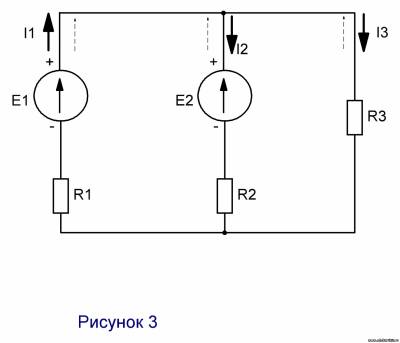
3. Метод двух узлов

Этот метод применим для схем, имеющих два узла

1. Выбираем произвольно направления токов в ветвях в одну и ту-же сторону (см. рис.3 – стрелки со штрихами).
2. Определяем проводимости ветвей:

                                      q₁=1/R₁=1/0,3=3,33 Сим.

                                      q₂=1/R₂=1 Сим.

                                      q₃=1/R₃=1/24=0,0416 Сим.

3. Определяем напряжение между двумя узлами по формуле:

                                      U=∑E_q/∑_arq=(E₁+E₂q₂)/(q₁+q₂+q₃)=(246∙3,31+230)/4,3716=240 В

4. Определяем токи в ветвях

                                     I=(E-U)q

                                     I₁=(E₁-U)q₁=(246-240)3,33=20A

                                     I₂=(E₂-U)q₂=230-240=-10A

                                     I₃=-Uq₃=240∙0,0416=-10А

Так как, значения I₂ и I₃ получились отрицательными, то эти токи будут противоположными по направлению (на рисунке показаны жирные сплошные стрелки).

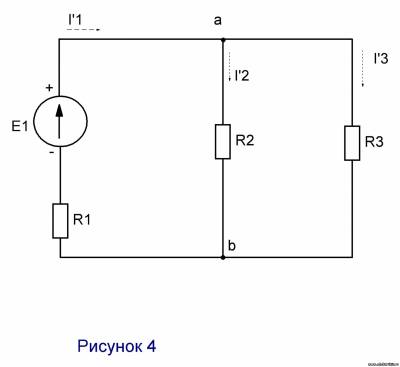
4. Метод наложения или метод суперпозиции

Метод основан на том, что любой ток в цепи создается совместным действием всех источников питания. Поэтому можно рассчитать частичные токи от действия каждого источника питания отдельно, а затем, найти истинные токи как арифметическую составляющую частичных.

Решение

1. Рис. 4. Е₂=0; r₂≠0

                                      R_э=R₂R₃/(R₂+R₃)+R₁=24/25+0,3=0,96+0,3=1,26 Ом

                                      I’₁=E₁/R_э=246/1,26=195,23 Ом

                                      U_ab=I’₁R₂₃=195,23∙0,96=187,42 В

                                      I’₂=U_ab/R₂=187,42 A

                                      I’₃= U_ab/R₃=187,42/24=7,8 A

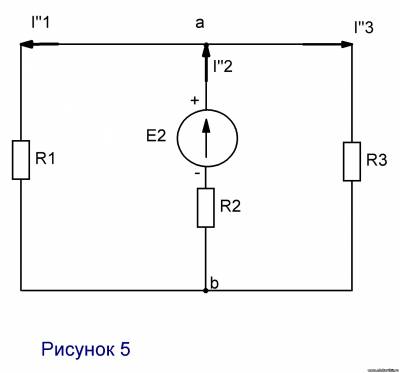
2. Рис. 5. E₁=0; R₁≠0

                                      R_э=R₁R₃/(R₁+R₃)+R₂=0,3∙24/24,3+1=0,29+1=1,29 Ом

                                       I”₂=E₂/R_э=230/1,29=178,29 A

                                       U_ab=I”₂R₁₃=178,29∙0,29=51,7 В

                                        I”₁=U_ab/R₁=51,7/0,3=172,4 A

                                        I”₃=U_ab/R₃=51,7/24=2,15 A

3. Определяем истинные токи.

                                        I₁=I’₁-I”₁=195,23-172,4=22,83 A

                                        I₂=I’₂-I”₂=187,42-178,29=9,13 A

                                        I₃=I’₃-I”₃=7,8-2,15=5,65 A