Метод преобразования треугольника и звезды сопротивлений - Начало. Основы. - Справочник

Метод преобразования треугольника и звезды сопротивлений

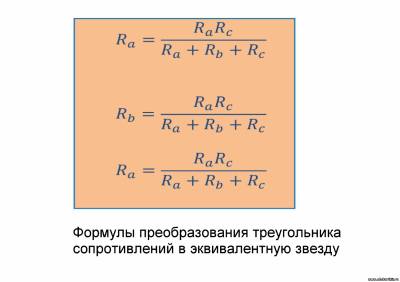
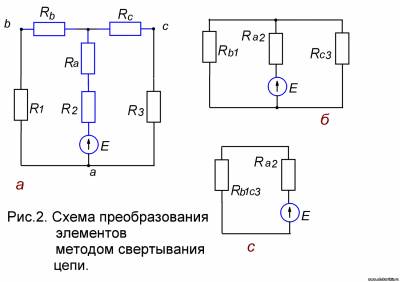
Метод преобразования треугольника и звезды сопротивлений 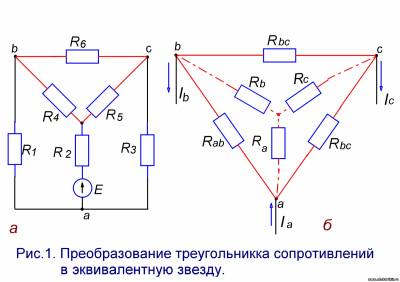На рисунке 1,а приведена схема, в которой прямую замену замыкающихся на разные узлы резисторов эквивалентным сопротивлением произвести нельзя. Здесь резисторы R4, R5 и R6 образуют треугольник (Δ), а сопротивления R2, R4 и R5 образуют звезду (y). Для расчета схемы в этом случае можно воспользоваться уравнением состояния узла и контура или преобразовать треугольник в звезду (рис.1, б). Тогда схема значительно упростится. Формулы преобразования треугольника в звезду получат следующий вид: Сопротивление луча эквивалентной звезды равно произведению сопротивления сторон треугольника, прилегающих к лучу, деленному на сумму сопротивлений всех сторон треугольника. Для замены звезды эквивалентным треугольником пользуются следующими формулами: Здесь сопротивление стороны треугольника равно сумме сопротивлений двух лучей звезды, опирающихся на это сопротивление, плюс произведение сопротивлений указанных лучей, деленное на сопротивление третьего луча звезды. Приведем простой пример. Определим общее сопротивление, если все значения резисторов будут по 3 Ома (см. рис.1, а). Сначала преобразуем треугольник сопротивлений R4R5R6 в эквивалентную звезду. Так как все значения резисторов одинаковы, возьмем R1=R2=R3=R4=R5=R6=x, тогда схема преобразования звезды примет вид (рис2, а): Далее преобразовываем схему по уже известному нами методу – методу свертывания цепи: 1. Сначала преобразовываем последовательные соединения (рис.2, б): (примем за y); 2. Затем сокращаем параллельные ветви Rb1и Rc3(рис.2, с): 3. Остается суммировать значения двух оставшихся сопротивлений: Подставляем вместо значения х наши 3 Ома и получаем:
1 2 3 4 5 Категория: Начало. Основы. \| Добавил: Электрик (15.12.2013)
Просмотров: 18669 \| Теги: треугольник сопротивлений, эквивалентная звезда \| Рейтинг: 5.0/2

Всего комментариев: 0